数学家们！十大基础数学证明，“简单”的蜂窝猜想证明，花了2000多年的时间( 二 )

亨利·庞加莱在1904年提出了这个猜想，并在2000年被评为千禧年奖问题之一。在20世纪50年代和60年代，其他数学家尝试证明这个猜想。
1958年，R. H. Bing证明了Poincaré猜想的一个弱版本：如果一个紧凑的3维流形的每个简单闭曲线都包含在一个3维球中，那么这个流形与3维球是同胚的。
俄罗斯数学家佩勒曼以汉密尔顿的里奇流理论为基础，利用Cheeger、Gromov和Perelman自己在度规空间上的结果，提出了一个完整的解决方案。该解决方案在2002年至2003年间在网上发布了三份预印本，并在2006年进行了审查和确认。
佩勒曼因其工作而被授予菲尔兹奖章。庞加莱猜想属于代数拓扑的早期历史。将该猜想推广到更高维度（已被证明）与黎曼几何中的变形概念有关，对万有引力和宇宙学具有启示和应用。
四色定理（124年）
该定理指出，四种颜色足以为任何地图上色，使两个相邻的区域不会共享相同的颜色。这个猜想是由弗雷德里克·格思里在1852年向他的教授、数学家奥古斯都·德·摩根提出的，后者将这个猜想公之于众，并对其解决方案做出了贡献。
在第二阶段，数学家们专注于寻找技术，将复杂的地图简化为一组可测试的可分类案例。最初，这个集合被认为包含将近9000个成员，所以数学家们求助于计算机技术来编写可以为他们做测试的算法。
1976年，阿佩尔和哈肯将测试问题简化为1936个构型，并在计算机的帮助下实现了四色猜想的完整解决方案。该定理在图论中得到了证明，欧拉公式起到了关键作用；然而，随着时间的推移，射影几何、结论、拓扑学和组合学对证明做出了贡献。
Catalan猜想（158年）

文章插图
数学家 Catalan在1844年推测，8和9是唯一的连续幂，即

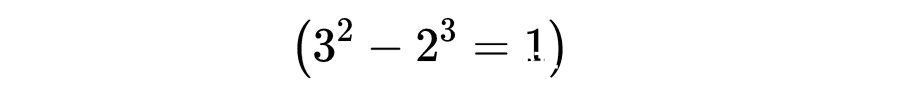
文章插图
换句话说，（8，9）是方程x^p - y^q =±1的唯一非平凡解。早在Catalan前500年，Levi ben Gerson就已经提出，平方数和3次方数相差为1的唯一满足条件的是8和9。Hyyr?和马可夫斯基证明了不存在三个连续的幂。蒂伊德曼在1976年指出，如果猜想不成立，可能只有有限数量的例外。
M. Mignotte在1999年证明，如果存在非平凡解，则p 猜想的推广应用于复数理论。其他的应用是在伽罗瓦群理论中。
费马大定理（358年）

文章插图
费马在1637年提出的猜想说，对于任何大于2的整数n，都不存在a, b, c这样的正整数满足a^n + b^n = c^n。这是数学史上最著名的定理之一，它可以用多种方法等价地表达出来，无论是在数论中还是在椭圆曲线理论中。
费马只是在n = 4的特殊情况下证明了这个猜想；然而，这产生了一个重要的简化，即充分证明指数n为质数的猜想。然后，数学家们花了350年的时间来寻找一个证明，他们中的许多人都取得了进展。
在费马的部分证明之后的两个世纪里，这个猜想只在质数3、5和7上得到了证明。在19世纪中叶，E. Kummer证明了所有正则质数都是如此。最后的证明是由A.怀尔斯在1995年提出的，他用伽罗瓦表示代替了椭圆曲线。这一证明为他带来了2016年的阿贝尔奖。在寻找解的过程中，我们发现了椭圆曲线和模形式这两个完全不同的数学领域之间的联系。这个问题及其解决方法促进了代数数论的发展和模性定理的证明。
开普勒猜想（403年）

文章插图
1611年，天文学家约翰内斯·开普勒提出了这一猜想，该猜想与三维空间中的球体堆积有关：它说，填充空间的同等大小的球体的平均密度，都比不上立方体紧密堆积和六边形紧密堆积的球体的平均密度。高斯在1831年证明，如果球体排列在一个规则的晶格中，这个猜想是正确的。